Kouzaki Measurement Registration & Judicial Scrivener Office
Kouzaki Measurement Registration & Judicial Scrivener Office
2015年12月19日
９．朔日等の計算 その２ （天体の位置の表し方（概略の説明））
今や、われわれは地球が太陽系の一員であり、自転しながら太陽の周りを公転してい
ること、太陽系自身も銀河系の一員であり、銀河の自転と共に運動していること、その他
さまざまなことを知っている。しかし、空の星を表すのに、やはり星々は観測者を中心と
した仮想上の球面上にあると考えた方が便利なことが多い。この仮想上の球面を天球と呼
んでいる。
そして、天球上の天体の位置を表すために、地球上の北極、南極の二つの極や赤道を
延長し、天球との交線を考えると、次の図のようになる。（観測者のいる位置は、中心Ｏ
である。）
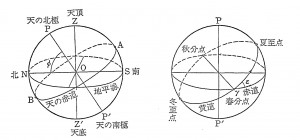
黄道は天球上の太陽の通り道である。天の赤道も黄道もともに球面上の大円であり、
二点で交わる。西回りに進む時、黄道が天の赤道を南から北に横切る点を春分点といい、
ギリシャ文字のγで表す事が多い。同様に夏至点、秋分点、冬至点が定義されるが、これ
らは黄道上の点である。
天球上、地球の経度、緯度と同様の目盛が刻まれていて、それぞれ赤経、赤緯と呼ば
れる。赤経のスタート点は春分点γであり、赤緯のスタート点は天の赤道である。（赤経
については、その単位は角度でも良いのだろうが、時間単位で表されるのが普通である。）
現在の時刻系は、天の赤道上に仮想天体を置き、一様なスピードで天の赤道上を運動
させた場合の、その天体の位置が基準になる。
同様に、基準面を天の赤道ではなく黄道にとった場合、天体の位置は黄径、黄緯で表
す事ができる。黄径は通常の角度単位である。球面三角法の公式を使えば、赤径、赤緯と
黄径、黄緯は相互に変換することができる。
黄道は、天球上の太陽の通り道であるから、実際の太陽は概ね黄道上にあると考えて
よい。（実際には様々な要因のため、黄緯も変化するが、大きな値ではない。）
月は、地球の周りを公転しながら、地球と一緒に太陽の周りをまわっている。月の天球
上の公転軌道を白道と呼ぶが、これは黄道とは５度程度しか傾いていない。日食や月食の
計算において、この傾きは大きな意味を持つが、これからの暦要素の計算においては、ほ
とんど無視して差し支えないと思われる。つまり、月も黄道から大きく離れる事はない。
朔（新月）とは、地球から見て、月、太陽の順に一列に並んでいる状態と考えられるか
ら、黄道上では月も太陽も同じ位置を占めている。つまり、それぞれの黄径が等しくなる
状態と考えてよい。
朔日の計算という目標が、少し具体的に見えてきた。太陽と月の黄径を計算し、それが
等しくなる「黄径」の値がわかれば、太陽がその黄径に至る日付は計算できるからである。
したがって、とりあえずはそれぞれの黄径を計算する必要がある。
９－２ 太陽と月の黄径
簡単に述べたが、本来これらの計算を厳密に実行する事は非常に困難であり、恐らく位
置天文学の専門書以外に適当な参考資料もない。もちろん私の手にも負えないので、最終
的に相応の精度で計算できる近似計算というところに落ち着いた。
ネット上では、さまざまな情報が公開されており、高精度の計算サイトも存在する。し
かし、自分で暦要素を求めるという目的から言うと、計算方法が公開されているものが望
ましい。海上保安庁海洋情報部のホームページ（＊２）をはじめ、このようなサイトもた
くさんある。また、（＊３，＊７）のように新月（朔）の日付を求める Java Script を
公開しているサイトもある。これらのサイトは大いに参考にさせていただいた。
［註 ＊２，＊３，＊７ 暦のはなし（１） 参考書籍等 参照］
黄径を計算するという目的から言えば、海上保安庁海洋情報部のホームページ（＊２）
の方法で、赤径、赤緯を計算し、黄径、黄緯に変換する方法が考えられるが、定期的に表
の入れ替えが必要になる点もあり、その方法論上、あまり長期の期間を対象にする事は難
しい。（＊１）は少しデータが古いけれど、この中に海上保安庁水路部（現海洋情報部）
で開発され、昭和５３年の天測暦に発表された、太陽と月の黄径の近似計算式が示されて
いる。実は、この後、天文システムの改訂があり、この式のまま計算して、どの程度の精
度が得られるのか多少の不安があったので、いくつかの例をピックアップして、例示的に
計算し比較してみた。
その結果として、この式は、精度的にも十分実用に耐えると判断したものである。
以下に、その計算式を示す。まずは太陽の黄径の略計算式である。
ここで、問題になりそうなのは変数Ｔであろう。この頃（昭和５３年頃）採用されてい
た時刻系は暦表時（ＥＴ）と呼ばれるものであり、現在は使われていない。この説明は長
くなるので、また別の機会とするが、Ｔはこの歴表時で１９７５年１月０日０時ＥＴから
観測時までの経過時間を３６５．２５日の単位で表したものである。
現在使用している時刻系を使って、このＴを求める方法も、長沢先生の本の中で丁寧に
解説されている。簡単に説明すると
観測時の年、月、日、時、分、秒（世界時）に対して
Ｗ＝（年－１９００）／４ を求める。この小数部分をＦとする。
Ｙ＝［１４６１Ｗ］，Ｘ＝［（月＋７）／１０］，Ｒ＝［１－Ｆ］，
Ｓ＝［０．４４（月＋４．４）］
を計算する。（ＦはＷの小数部分、［ ］はガウス関数と呼ばれ中の数を超えない最大の
整数を表す。）以上の準備で、観測時０時までの経過日数Ｚを求める事ができる。（次式）
Ｚ＝Ｙ＋３１×月＋日＋（Ｘ－１）Ｒ－ＸＳ－２７４２４ 後は時間について
Ｊ＝時／２４＋分／１４４０＋秒／８６４００ とすれば世界時の経過時間 ｔ は
ｔ＝（Ｚ＋Ｊ）／３６５．２５ となる。これを歴表時に変換する。近似であるが
Ｔ＝ｔ＋（０．０３１７ｔ＋１．４３）×１０＾（－６） という手順である。
上が、月の黄径の近似計算式である。（出典は同じ、Ｔの意味も同様である。）太陽に
比べて遥かに複雑であることが、一目見た項数だけでもお分かりいただけるだろう。地球
と太陽だけではなく、月は色々な天体の影響を受け、極めて複雑な運動をしている事がわ
かる。
９－３ 朔日を求める
上記の近似式を基本として、観測日（年、月、日）と観測時刻（時、分、秒）からまず
Ｔ（９－２参照）を求める。そのＴを使って、太陽黄径Ｓ（Ｔ）と月の黄径Ｍ（Ｔ）を計
算する。太陽は凡そ一年かけて黄道を一周するから、黄径の増加は一日当たり平均すれば
１度に満たない。月は凡そ２９．５日で黄道を一周するから、黄径の増加は一日当たり
１０度を超える。
観測日を含めた意味での、観測日より前の朔の日付を求めるためには、両天体を逆向き
に動かす事になる。従って Ｍ（Ｔ）－Ｓ（Ｔ） を計算し、これを両者の黄径の増加
量の差で割り、その値を観測日に補正する（遡るので、引き算である。）
簡単にいえば、このプロセスの繰り返しで、Ｓ（Ｔ）＝Ｍ（Ｔ） となるＴ、従ってそ
の元となった日付、時間を確定する事が出来る。その日付、時間が朔の日、時間に他なら
ない。（元になっているのがあくまでも近似式であるから、多少の誤差は覚悟する必要が
ある。）
一番オーソドックスと思われる手順であるが、一つメリットがある。というのは、太陽
の黄径＋α の位置に仮想の点を置き、その点と月との間で同様の手順を考えると、太陽
と月の黄径差がαになる日時を求めることができる。
α＝０ の時が朔（新月）であり、α＝１８０度 の時が満月である。任意の角度αに
対してその日時を求める事ができるわけである。
余計な話であるが、中秋の名月は旧暦８月１５日の月であり、必ずしも満月とは限らな
い事も確かめる事ができる。
